Þ 2 étapes majeures : Etape DATA et étape PROC

DATA : import des données, saisie des données, manipulation des données.

PROC : traitement des données ; tous les outils d’analyse des données disponibles dans SAS, des statistiques jusqu’aux graphiques.

Þ Organisation du logiciel : on utilise un fichier de commandes, avec le langage SAS.

La table SAS est une matrice croisant les observations en lignes aux variables en colonnes.

Les tables sont stockées dans les librairies (ou bibliothèques).

1 table est temporaire (placée dans la bibliothèque WORK, détruite à la fin de la session SAS) par défaut, mais peut être permanente.

Þ Les types de variables reconnus par SAS

Les variables qualitatives ou character

Les variables quantitatives ou numeric

Remarque : les commandes SAS apparaissent en gras à ex : libname / format / set / run…

Les champs à remplir apparaissent en italique à ex : data nom de table…

Þ L’instruction run ;

Elle doit être placée à la fin de chaque étape du fichier de commande. C’est la demande d’exécution.

àDéfinition d’une nouvelle librairie (bibliothèque) : libname nom_de_librairie ‘emplacement du répertoire physique’ ;

Ex : libname fleurs ‘C:\MesDocuments’ ;

àStockage permanent de la table dans une librairie : data nom_de_librairie.nom_de_table ;

set nom_de_table ;

Ex: data fleurs.iris;

set iris;

run;

data nom_de_table ;

Input nom_de_variable_qualitative1 $ nom de variable quantitative1 nom de variable quantitative2… ;

Datalines ; (ou cards ;)

<Saisie des valeurs des variables, observation 1>

<Saisie des valeurs des variables, observation 2>

… ; Run ;

data nom_de_table ;

Infile fichier_en_entrée ; /* par exemple C:\fichier.txt ou fichier.dat */

Input format de lecture ;

Run ;

Þ Les options de Input : @n (lit la variable à partir du n-ième caractère).

n. (lit la variable pendant n caractères)

n-m (lit la variable du n-ième au m-ième caractère)

n .2 (divise le n-ième caractère par 10²)

missover (détecte les valeurs manquantes et les remplace par des .)

$ (la variable est qualitative)

Ex : Input @1 no 1. @3 nss 15. nom $ 18-20

àà partir du premier caractère du fichier on lit la variable no (type numéric, longueur1)

àà partir du 3^ème caractère, et long de 15 caractères, on lit la variable nss (type numéric)

àdu 18^ème caractère au 20^ème, on lit la variable nom (type character)

Remarque : la lecture la plus fiable est n-m, qui précise la colonne de début et de fin.

Remarque : il est possible d’éditer un fichier texte à partir d’une table SAS avec la commande Put.

Label nom_de_variable = « libellé associé » ;

àCréation de variable : data nom_de_table ;

Set nom_de_table ;

Nouvelle_variable = calcul sur variable existante ;… ; run ;

Ex : Lop2= exp(lop+2) (nelle variable Lop2 : ajout de 2 aux valeurs que prend la variable lop, et on passe à l’exponentielle)

àForcer le type d’une nouvelle variable : length nom_de_variable $n; /*la variable sera de type caractère ; n caractères max*/

length nom_de_variable n.; /*variable numérique sur n octets*/

Ex : length Nbfs 3. ;

Nbfs=Q26+Q27 ;

àSélection des observations : if condition

Ex : if lop>2 (la table créée contiendra les observations sur toutes les variables, filtrées par la valeur lop>2)

àL’ instruction if condition then effet;

Else;

Ex: if lop>2 then Lop2=1;

Else Lop2=0; (la nouvelle variable Lop2 vaut 1 si lop>2)

àL’instruction do ;

instructions ;

End ;

Þ Les options de l’instruction do :

Do i=entier to i=entier; instructions ; end;

Do while(condition) ; instructions ;end ; /*boucle tant que le test est vrai*/

Do until(condition) ; instructions ;end ; /*boucle jusqu’à ce que le test soit vrai*/

àPour réaliser des modifications ou opérations sur un groupe de variables de la table

àarray tab{nombre de variables} <$> liste des variables ; /*déclaration du tableau, mettre $ si variables de type caractère*/

Ex : array tab{22} $ Q22- -Q30f ;

Do i=1 to 22 ;

If tab{i}=”n”  then tab{i}=”N”;

If…

End;

Ex : var1= « a » ;var2= « b » ;var3= « c » ;

Tout=var1||var2||var3 ; /*Tout= « abc »*/

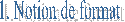
àassocier une modalité à son libellé, regrouper plusieurs modalités sous 1 même libellé

Il y a deux étapes dans les gestions de format à 1. Création et gestion de format (PROC FORMAT)

2. Utilisation des formats (instructions de FORMAT)

Proc format data = nom_de_table <options> ;

Value <$>nom_de_format /* $ pour un format qui s’applique à une variable caractère*/

Liste de valeurs = ‘libellé 1’

…

Liste de valeurs = ‘libellé n’

Run ;

Þ Les options de value : Valeur1=’libellé’ (libellé d’une valeur simple)

Valeur2-valeur10=’libellé’ (libellé d’une liste continue de valeurs)

Valeur3,valeur5,valeur10=’libellé’ (libellé d’une liste exhaustive de valeurs)

Valeur1,valeur3,valeur5-valeur10=’libellé’ (libellé d’une liste discontinue de valeurs)

Low = ‘la plus petite valeur rencontrée’

High = ‘la plus grande’

Other : ‘toutes les valeurs non prévues dans les autres classes’

Format nom_de_variable <$> nom_de_format. ; /* on utilise format en étape data ou lors d’un PROC utilisant la variable*/

/* Attention au point après nom_de_format */

Ex : regroupement d’âges en classes quinquennales sur une variable « age » d’une table SAS

Proc format;

Value quin

Low-14 = ‘0 à 14 ans’

15-19 = ’15 à 19 ans’

20-24 = ’20 à 24 ans’

…

40-High = ’40 ans et plus’

122 = ‘Jeanne Calment’

Run ;

/* on pourra maintenant se servir du format « quin » avec la commande Format age quin. ; */

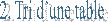(par défaut la table est remplacée, on peut en créer une nouvelle avec out)

Proc sort data = nom_de_table< out = nouveau_nom_de_table> ;

By descending variable1… ascending variable n; /* ascending par défaut */

Run;

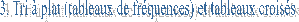
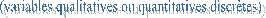
Proc freq data = nom_de_table <liste d’options> ;

By Liste de variables ; /* demande de tableau trié */

Tables variable1 var2 var3*var4 /<liste d’options> ; /*si on veut un tableau croisé on sépare les variables par * */

Where condition /*restriction du tableau selon la condition*/

Weight variable ; /* si il y a une variable de pondération */

Run ;

Þ Les options de tables : out = nom_de_table ; (stockage des résultats dans une table SAS)

Missing ; (on compte les non-réponses)

Nopercent ; (ne pas afficher les résultats en pourcentage de l’effectif total)

Nocol, Norow, Nofreq…

Chisq ; (statistique du khi-2, test d’indépendance des variables si tableau croisé)

Proc freq data = nom_de_table <liste d’options> ;

Table var1*var2*var3 ; /*associés à chaque modalité de q1, on obtient les tableaux croisés de var2*var3*/

Run ;

Proc freq data = nom_de_table <liste d’options> ;

Table q1- -q50 ; /*tris à plat de toutes les variables de q1 à q50*/

Run ;

Proc print data = nom_de_table <liste d’options> ;

Var var1 var2... ; /*liste des variables à afficher*/

Where var1 <not> in (modalité1 de var1,modalité2,...) ; /* ne (pour not equal) si une seule modalité*/

Run ;

àPour connaître le nombre de variables de la base, leur position, leur type, leur taille...

Proc contents data = nom_de_table <position... (liste d’options)> ;

Run ;

Proc means data = nom_de_table <liste d’options> ;

Class liste de variables; /* sorties plus lisibles qu’avec by, et affiche les effectifs des sous populations*/

Var liste de variables quantitatives ; /* la seule instruction obligatoire */

By liste de variables;

FREQ variable; /*tableau de fréquences de la variable*/

WEIGHT variable;

ID variable; /* mentionne la valeur maximum de la variable pour chaque groupe défini par class */

Output out=nom_de_table <statistiques à conserver>;

Run ;

Proc univariate data = nom_de_table<liste d’options> ;… (les commandes sont les mêmes que proc means)

Þ Les options de proc univariate : plot ; (diagrammes)

Freq ; (donne un tableau de fréquences) variable ;

à La procédure Proc Tabulate permet de construire des tableaux hiérarchiques de résumés statistiques de façon condensée.

Les tableaux peuvent être dimensionnés selon trois axes : PAGE, LIGNE, COLONNE. Chaque axe peut combiner différentes variables selon différents modes.

Le tableau se construit en calculant certaines statistiques pour une ou plusieurs variables quantitatives (appelées d’analyse ici) pour chaque sous-ensemble déterminé par la combinaison des variables de classification (qualitatives ou quantitatives discrètes).

Chaque cellule correspond finalement à une statistique calculée pour une variable d'analyse pour un certain sous-ensemble.

Proc tabulate data = nom_de_table<liste d’options> ;

Class liste de variable ; /* contient la liste de toutes les variables utilisées pour définir les sous-ensembles */
Var liste des variables d’analyse ; /* contient les variables d'analyse. Si elle est omise, on applique la statistique N soit le nombre d’observation avec données non manquantes pour la variable d’analyse.*/
Table << expression page, > expression ligne, > expression colonne / <liste option table > ;

By liste de variables; /* variables définissant les sous-populations */

FREQ variable ; /*variable de répétition de l'observation, ou fréquence de l’observation */

Keylabel motclé1=' libellé1' motclé2=’libellé2’ … ; /* par exemple N=’effectif’ ; */

WEIGHT variable;

Run ;

Þ Les expressions de Table : elles déterminent la forme du tableau et le type de statistiques calculées

pour la variable d’analyse.

àLes variables de classification peuvent être reliées entre elles par trois opérations et cela détermine la forme du tableau.

SEXE * ETAT F M

1 2 3 4 1 2 3 4

SEXE ETAT F M  1 2 3 4

SEXE * ( ETAT LIEN )

F M

1 2 3 4 a b c 1 2 3 4 a b c

ETAT * SEXE * LIEN

1 2 3 4

F M F M F M F M

a b c a b c a b c a b c a b c a b c a b c a b c

Imbrication :Table var1 * var2 ;

Concaténation liste simple : Table var1 var2 ;

Groupage : Table (var1 var2) ;

Ex. si l'on considère trois variables suivantes :

SEXE prenant les valeurs M ou F

ETAT prenant les valeurs 1, 2, 3 ou 4

LIEN prenant les valeurs a, b ou c

àLes axes ou dimensions : PAGE, LIGNE, COLONNE sont séparées par une virgule.

-S'il n'y a qu'un axe, il s'agira de colonnes.
-S'il n'y a que deux axes, il s'agira de lignes et colonnes.
-S'il y a trois axes, il s'agira de pages, lignes et colonnes.

àLe choix des statistiques qui concernent la variable d’analyse :

MAX valeur maximum
MEAN moyenne arithmétique
MIN valeur minimum
N nombre d'observations ayant une valeur non manquante pour la variable d'analyse
NMISS nombre d'observations ayant une valeur manquante pour la variable d'analyse
PCTN pourcentage des fréquences
PCTSUM pourcentage de la somme
PRT probabilité d'une valeur absolue plus grande pour la valeur t
RANGE domaine des valeurs, MAX-MIN
STD écart type
STDERR erreur type de la moyenne
SUM somme
SUMWGT somme pondérée
USS somme des carrés non corrigée
T valeur T de Student pour tester l'hypothèse d'une moyenne nulle de la population
VAR variance

Ex : Var AGE ;

Table ETAT , SEXE*AGE*(min mean max); /*la variable d’analyse est AGE, donc on obtient les moyennes d’age des individus, les ages min et max de la table répartis par sexe et par état (en lignes), donc en 2 dimensions*/

àRemarques

Table AGE all, SEXE all /* all permet d’ajouter les totaux dans les marges pour les variables concernées, soit les résultats pour toutes les modalités regroupées */

L'absence de demande de statistique équivaut à la demande de la somme SUM.
L'absence de variable d'analyse équivaut à la demande du décompte N.

Þ 1 lien pour plus d’informations et des exemples avec PROC TABULATE.

Le but de ce type d’analyse est d’étudier les liens entres des variables. On distingue les variables explicatives et les variables à expliquer. On utilise des « tests statistiques », ce qui entraîne des résultats plus approfondis qu’avec les statistiques descriptives obtenues par les tableaux croisés (ou de fréquence) par exemple. En effet on obtient, sous certaines hypothèses, des résultats qui concerne la population globale, plus seulement celle de l’échantillon.

Le traitement est différent selon le type des variables analysées.

3 modèles sont présentés dans le cours : L’étude du lien entre variables qualitatives

L’étude du lien entres variables quantitatives

L’étude du lien entres variables qualitatives et quantitatives (comparaison de moyennes)

Þ Formuler une question concernant le lien entre deux variables qualitatives V1 et V2

Ex : y a t il un lien entre la connaissance de la contraception et le lieu de vie à Madagascar ?

Þ Etudier le tri à plat de chaque variable (Proc freq, Proc gchart pour les distributions graphiques)

A cette étape il est nécessaire de regrouper les modalités de poids trop faible si cela a un sens.

Trier les données.

Þ Test d’indépendance des variables (Test du Chi-2)

Conditions du test :

l’échantillon doit comporter 30 observations au minimum

l’effectif de chaque sous-groupe (effectifs marginaux) du tableau croisé des 2 variables doit être supérieur à 5

Hypothèses :

H0 à les variables V1 et V2 sont indépendantes dans la population totale

H1 à dépendance

Statistique de test : loi du Chi-2 à (Nombre Lignes-1)*(Nombre Colonnes-1) degrés de liberté, sous H0.

Conclusion : rejet ou non de H0.

Statistique	DDL	Valeur	Prob.
Khi-2	1	3.57	0.059

H0 est vraie si : Chi-2Obs est inférieur ou égal à Chi-2(z,alpha) – z degrés de liberté, alpha le risque d’erreur-

Si l'on se fixe un risque d'erreur alpha=10%, la valeur théorique du Chi-2 correspondant à 1 ddl est Chi-2(1,0.1)= 2.71.

La valeur du Chi-2 observé étant de 3.57, on peut rejeter H0 et affirmer avec un risque d'erreur de 10% que V1 et V2 ne sont pas distribués au hasard l'un par rapport à l'autre.
Si l'on se fixe un risque d'erreur plus faible, alpha=5%, la valeur du Chi-2 théorique est Chi-2(1,0.05)= 3.84 et l'on ne peut plus rejeter H0. On conclue alors qu'il n'est pas possible d'affirmer qu'il existe une relation entre les deux caractères V1 et V2, sauf à admettre un risque d'erreur supérieur à 5%.

à SAS détermine la valeur minimale de alpha permettant de rejeter H0. (Prob.)

Plus cette valeur est faible, plus on peut affirmer avec un faible risque d'erreur qu'il existe une relation entre les deux caractères. Cette valeur minimum de rejet de H0 est donc inversement proportionnelle à la significativité de la relation entre les deux caractères étudiés. Dans notre exemple la valeur minimum de alpha est de 0.059 ce qui implique un risque d'erreur de 6% lorsque l'on rejette H0. La relation n'est donc pas très significative et on ne peut pas affirmer avec certitude qu'il existe un lien entre V1 et V2.

Seuil de rejet de H0	Relation  ...	Symbole
> 0.10	... non significative	-
0.05 à 0.10	... peu significative	*
0.01 à 0.05	... significative	**
0.001 à 0.01	... très significative	***
0.001 <	... extrêmement significative	****

Syntaxe :

Proc freq data = nom_de_table <liste d’options> ;

By V1 ou V2 ; /* demande de tableau trié */

Tables V1*V2 / chisq <liste d’options>; /*options : no row no percent no freq */

Weight variable ; /* si il y a une variable de pondération */

Run ;

Þ Pour aller plus loin si les variables ne sont pas indépendantes

On lit le V de Cramer : Compris entre 0 (indépendance) et 1(dépendance)

Les V de Cramer inférieurs à 0.020 sont considérés comme trop faibles. Ils indiquent que le lien

entre les deux variables est trop faible pour mériter d'être pris en compte.

V= √ (Chi-2Obs / (n*min(nb lignes, nb colonnes)))

Þ poser une question qui met en relation var. qualitative et var quantitative

ex : les femmes en milieu rural ont-elles autant d’enfants que les femmes en milieu urbain ?

hypothèse : il y a + d’enfants en milieu rural

Þ opérationnalisation des variables

V102 : milieu de résidence

V209 : naissances ayant eu lieu l’année précédent l’enquête

On compare les moyennes

H0 : moy des fe rural = moy des fe urbain

H1 : différent

Les effectifs de chaque sous-groupe de la variable qualitative doivent être > 30

Þ comparaison des moyennes:

proc ttest data = nom_de_table;

class variable qualitative; /* V102 */

var variable quantitative; /* V209 */

run ;

Le risque minimum associé au rejet de H0 est <0.001

On rejette donc H0 : les moyennes sont significativement différentes à rural>urbain

Proc gchart data=nom_de_table ;

vbar liste de variables à représenter / <liste d’options> ; /* pour un histogramme en barres verticales */

by variable ;

run ;

Þ Les choix de tracés (à la place de vbar)

Block liste de variables à représenter ;  /* barres à 3 dimensions */

hbar liste de variables à représenter ; /* histogramme, barres horizontales */

pie liste de variables à représenter ; /* camemberts */

star liste de variables à représenter ; /* graphiques étoilés */

Þ Les options

Discrete : Il est important de spécifier l’option discrete pour les variables qui ont été recodées par la procédure proc format, sinon le programme essaiera de créer des classes.

Levels : Lorsque la variable principale est une variable quantitative, on peut laisser SAS créer les classes à représenter. Mais aussi spécifier combien de classes retenir, par l’options levels= nombre de classes à retenir.

Missing : prend en compte les valeurs manquantes.

Proc gplot data = nom_de_table ;

plot variable1*variable2;

Run;

Þ Substr(nom_variable,position du 1^er caractère,longueur de la chaine extraite)

Pour extraire une sous chaine de caractères à partir d’une chaine de caractères

Ex : Datenais= « 1990 » ;

A=substr(Datenais,3,2) ;  /*le résultat est donc A= « 90 »*/

Þ Index(nom_variable,caractère recherché) /*renvoie un entier*/

Pour connaître la position d’un caractère dans une chaine de caractère(renvoie 0 si le caractère est absent)

Ex : B=Index(Datenais, « 0 ») /*=4*/

Þ Round(entier, 1) /*100 10 1 .01 .001*/

Pour arrondir une valeur ou les valeurs d’une variable

Ex : Round(2187.23,100) /* =2000 */

Round(2187.23,0.1) /* =2187.2 */

Þ Max et Min

Pour connaître le max ou le min d’un groupe de variables numériques

Ex : Max(Q1,Q2,Q3)